Carleman's equation
In mathematics, Carleman's equation is a Fredholm integral equation of the first kind with a logarithmic kernel. Its solution was first given by Torsten Carleman in 1922. The equation is
The solution for b − a ≠ 4 is
If b − a = 4 then the equation is solvable only if the following condition is satisfied
In this case the solution has the form
where C is an arbitrary constant.
For the special case f(t) = 1 (in which case it is necessary to have b − a ≠ 4), useful in some applications, we get
References
- CARLEMAN, T. (1922) Uber die Abelsche Integralgleichung mit konstanten Integrationsgrenzen. Math. Z., 15, 111–120
- Gakhov, F. D., Boundary Value Problems [in Russian], Nauka, Moscow, 1977
- A.D. Polyanin and A.V. Manzhirov, Handbook of Integral Equations, CRC Press, Boca Raton, 1998. ISBN 0-8493-2876-4
This article is issued from Wikipedia - version of the 3/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
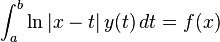
![y(x)
=
\frac{1}{\pi^2 \sqrt{(x-a)(b-x)}}
\left[
\int_a^b \frac{\sqrt{(t-a)(b-t)} f'_t(t) \, dt}{t-x}
+\frac{1}{\ln \left[ \frac{1}{4} (b-a) \right]} \int_a^b \frac{f(t) \, dt}{\sqrt{(t-a)(b-t)}}
\right]](../I/m/4b9e6c36d83286581f51af5110da8752.png)
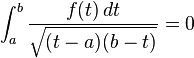
![y(x)
=
\frac{1}{\pi^2 \sqrt{(x-a)(b-x)}}
\left[
\int_a^b \frac{\sqrt{(t-a)(b-t)} f'_t(t) \, dt}{t-x}
+C
\right]](../I/m/94318cc9811f96e698f00dd3f03d5ab7.png)
![y(x)
=
\frac{1}{\pi \ln \left[ \frac{1}{4} (b-a) \right]} \frac{1}{\sqrt{(x-a)(b-x)}}](../I/m/442713404627b0ad7b97baa79654e52e.png)