Converse nonimplication

In logic, converse nonimplication^[1] is a logical connective which is the negation of the converse of implication.

Definition

$\scriptstyle {p\not \subset q}\!$ which is the same as $\scriptstyle {\sim (p\subset q)}\!$

Truth table

The truth table of $\scriptstyle {p\not \subset q}\!$ .^[2]


p	q	⊄
T	T	F
T	F	F
F	T	T
F	F	F

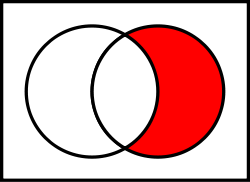
Venn diagram

The Venn Diagram of "It is not the case that B implies A" (the red area is true).

Also related to the relative complement (set theory), where the relative complement of A in B is denoted B ∖ A.

Properties

falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of converse nonimplication

Symbol

Alternatives for $\textstyle {p\not \subset q}$ are

$\textstyle {p{\tilde {\leftarrow }}q}$ : $\textstyle {\tilde {\leftarrow }}$ combines Converse implication's left arrow( $\textstyle {\leftarrow }$ ) with Negation's tilde( $\textstyle {\sim }$ ).
$\textstyle {Mpq}$ : uses prefixed capital letter.
$\textstyle {p\nleftarrow q}$ : $\textstyle {\nleftarrow }$ combines Converse implication's left arrow( $\textstyle {\leftarrow }$ ) denied by means of a stroke( $/$ ).

Natural language

Rhetorical

"not A but B"

Boolean algebra

Converse Nonimplication in a general Boolean algebra is defined as $\scriptstyle {q\nleftarrow p=q'p}\!$ .

Example of a 2-element Boolean algebra: the 2 elements {0,1} with 0 as zero and 1 as unity element, operators $\scriptstyle {\sim }\!$ as complement operator, $\scriptstyle {_{\vee }}\!$ as join operator and $\scriptstyle {_{\wedge }}\!$ as meet operator, build the Boolean algebra of propositional logic.

$\scriptstyle {\sim x}\!$	$1$	$0$
$x$	$0$	$1$

and

$y$
$1$	$1$	$1$
$0$	$0$	$1$
$\scriptstyle {y_{\vee }x}\!$	$0$	$1$	$x$

and

$y$
$1$	$0$	$1$
$0$	$0$	$0$
$\scriptstyle {y_{\wedge }x}\!$	$0$	$1$	$x$

then

\scriptstyle {y\nleftarrow x}\!

means

$y$
$1$	$0$	$0$
$0$	$0$	$1$
$\scriptstyle {y\nleftarrow x}\!$	$0$	$1$	$x$

(Negation)

(Inclusive Or)

(And)

(Converse Nonimplication)

Example of a 4-element Boolean algebra: the 4 divisors {1,2,3,6} of 6 with 1 as zero and 6 as unity element, operators $\scriptstyle {^{c}}\!$ (codivisor of 6) as complement operator, $\scriptstyle {_{\vee }}\!$ (least common multiple) as join operator and $\scriptstyle {_{\wedge }}\!$ (greatest common divisor) as meet operator, build a Boolean algebra.

$\scriptstyle {x^{c}}\!$	$6$	$3$	$2$	$1$
$x$	$1$	$2$	$3$	$6$

and

$y$
$6$	$6$	$6$	$6$	$6$
$3$	$3$	$6$	$3$	$6$
$2$	$2$	$2$	$6$	$6$
$1$	$1$	$2$	$3$	$6$
$\scriptstyle {y_{\vee }x}\!$	$1$	$2$	$3$	$6$	$x$

and

$y$
$6$	$1$	$2$	$3$	$6$
$3$	$1$	$1$	$3$	$3$
$2$	$1$	$2$	$1$	$2$
$1$	$1$	$1$	$1$	$1$
$\scriptstyle {y_{\wedge }x}\!$	$1$	$2$	$3$	$6$	$x$

then

\scriptstyle {y\nleftarrow x}\!

means

$y$
$6$	$1$	$1$	$1$	$1$
$3$	$1$	$2$	$1$	$2$
$2$	$1$	$1$	$3$	$3$
$1$	$1$	$2$	$3$	$6$
$\scriptstyle {y\nleftarrow x}\!$	$1$	$2$	$3$	$6$	$x$

(Codivisor 6)

(Least Common Multiple)

(Greatest Common Divisor)

(x's greatest Divisor coprime with y)

Properties

Non-associative

$\scriptstyle {r\nleftarrow (q\nleftarrow p)=(r\nleftarrow q)\nleftarrow p}$ iff $\scriptstyle {rp=0}$ ^[3] (In a two-element Boolean algebra the latter condition is reduced to $\scriptstyle {r=0}$ or $\scriptstyle {p=0}$ ). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative.

{\begin{aligned}(r\nleftarrow q)\nleftarrow p&=r'q\nleftarrow p&{\text{(by definition)}}\\&=(r'q)'p&{\text{(by definition)}}\\&=(r+q')p&{\text{(De Morgan's laws)}}\\&=(r+r'q')p&{\text{(Absorption law)}}\\&=rp+r'q'p\\&=rp+r'(q\nleftarrow p)&{\text{(by definition)}}\\&=rp+r\nleftarrow (q\nleftarrow p)&{\text{(by definition)}}\\\end{aligned}}

Clearly, it is associative iff $\scriptstyle {rp=0}$ .

Non-commutative

$\scriptstyle {q\nleftarrow p=p\nleftarrow q\,}\!$ iff $\scriptstyle {q=p\,}\!$ .^[4] Hence Converse Nonimplication is noncommutative.

Neutral and absorbing elements

$0$ is a left neutral element ( $\scriptstyle {0\nleftarrow p=p}\!$ ) and a right absorbing element ( $\scriptstyle {p\nleftarrow 0=0}\!$ ).
$\scriptstyle {1\nleftarrow p=0}\!$ , $\scriptstyle {p\nleftarrow 1=p'}\!$ , and $\scriptstyle {p\nleftarrow p=0}\!$ .
Implication $\scriptstyle {q\rightarrow p}\!$ is the dual of Converse Nonimplication $\scriptstyle {q\nleftarrow p}\!$ .^[5]

Converse Nonimplication is noncommutative
Step	Make use of	Resulting in
$\scriptstyle \mathrm {s.1}$	Definition	$\scriptstyle {q{\tilde {\leftarrow }}p=q'p\,}\!$
$\scriptstyle \mathrm {s.2}$	Definition	$\scriptstyle {p{\tilde {\leftarrow }}q=p'q\,}\!$
$\scriptstyle \mathrm {s.3}$	$\scriptstyle \mathrm {s.1\ s.2}$	$\scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q'p=qp'\,}\!$
$\scriptstyle \mathrm {s.4}$		$\scriptstyle {q\,}\!$	$\scriptstyle {=\,}\!$	$\scriptstyle {q.1\,}\!$
$\scriptstyle \mathrm {s.5}$	$\scriptstyle \mathrm {s.4.right}$ - expand Unit element		$\scriptstyle {=\,}\!$	$\scriptstyle {q.(p+p')\,}\!$
$\scriptstyle \mathrm {s.6}$	$\scriptstyle \mathrm {s.5.right}$ - evaluate expression		$\scriptstyle {=\,}\!$	$\scriptstyle {qp+qp'\,}\!$
$\scriptstyle \mathrm {s.7}$	$\scriptstyle \mathrm {s.4.left=s.6.right}$	$\scriptstyle {q=qp+qp'\,}\!$
$\scriptstyle \mathrm {s.8}$		$\scriptstyle {q'p=qp'\,}\!$	$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {qp+qp'=qp+q'p\,}\!$
$\scriptstyle \mathrm {s.9}$	$\scriptstyle \mathrm {s.8}$ - regroup common factors		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q.(p+p')=(q+q').p\,}\!$
$\scriptstyle \mathrm {s.10}$	$\scriptstyle \mathrm {s.9}$ - join of complements equals unity		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q.1=1.p\,}\!$
$\scriptstyle \mathrm {s.11}$	$\scriptstyle \mathrm {s.10.right}$ - evaluate expression		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q=p\,}\!$
$\scriptstyle \mathrm {s.12}$	$\scriptstyle \mathrm {s.8\ s.11}$	$\scriptstyle {q'p=qp'\ \Rightarrow \ q=p\,}\!$
$\scriptstyle \mathrm {s.13}$		$\scriptstyle {q=p\ \Rightarrow \ q'p=qp'\,}\!$
$\scriptstyle \mathrm {s.14}$	$\scriptstyle \mathrm {s.12\ s.13}$	$\scriptstyle {q=p\ \Leftrightarrow \ q'p=qp'\,}\!$
$\scriptstyle \mathrm {s.15}$	$\scriptstyle \mathrm {s.3\ s.14}$	$\scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q=p\,}\!$

Implication is the dual of Converse Nonimplication
Step	Make use of	Resulting in
$\scriptstyle \mathrm {s.1}$	Definition	$\scriptstyle {dual(q{\tilde {\leftarrow }}p)\,}\!$	$\scriptstyle {=\,}\!$	$\scriptstyle {dual(q'p)\,}\!$
$\scriptstyle \mathrm {s.2}$	$\scriptstyle \mathrm {s.1.right}$ - .'s dual is +		$\scriptstyle {=\,}\!$	$\scriptstyle {q'+p\,}\!$
$\scriptstyle \mathrm {s.3}$	$\scriptstyle \mathrm {s.2.right}$ - Involution complement		$\scriptstyle {=\,}\!$	$\scriptstyle {(q'+p)''\,}\!$
$\scriptstyle \mathrm {s.4}$	$\scriptstyle \mathrm {s.3.right}$ - De Morgan's laws applied once		$\scriptstyle {=\,}\!$	$\scriptstyle {(qp')'\,}\!$
$\scriptstyle \mathrm {s.5}$	$\scriptstyle \mathrm {s.4.right}$ - Commutative law		$\scriptstyle {=\,}\!$	$\scriptstyle {(p'q)'\,}\!$
$\scriptstyle \mathrm {s.6}$	$\scriptstyle \mathrm {s.5.right}$		$\scriptstyle {=\,}\!$	$\scriptstyle {(p{\tilde {\leftarrow }}q)'\,}\!$
$\scriptstyle \mathrm {s.7}$	$\scriptstyle \mathrm {s.6.right}$		$\scriptstyle {=\,}\!$	$\scriptstyle {p\leftarrow q\,}\!$
$\scriptstyle \mathrm {s.8}$	$\scriptstyle \mathrm {s.7.right}$		$\scriptstyle {=\,}\!$	$\scriptstyle {q\rightarrow p\,}\!$
$\scriptstyle \mathrm {s.9}$	$\scriptstyle \mathrm {s.1.left=s.8.right}$	$\scriptstyle {dual(q{\tilde {\leftarrow }}p)=q\rightarrow p\,}\!$

Computer science

An example for converse nonimplication in computer science can be found when performing a right outer join on a set of tables from a database, if records not matching the join-condition from the "left" table are being excluded.^[6]

References

↑ Lehtonen, Eero, and Poikonen, J.H.
↑ Knuth 2011, p. 49
↑
↑
↑
↑ http://www.codinghorror.com/blog/2007/10/a-visual-explanation-of-sql-joins.html

Knuth, Donald E. (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 (1st ed.). Addison-Wesley Professional. ISBN 0-201-03804-8.

Logical connectives

Tautology $\top$

NAND $\uparrow$ Converse implication $\leftarrow$ Implication $\rightarrow$ OR $\lor$

Negation $\neg$ XOR $\oplus$ Biconditional $\leftrightarrow$ Statement

NOR $\downarrow$ Nonimplication $\nrightarrow$ Converse nonimplication $\nleftarrow$ AND $\land$

Contradiction $\bot$

This article is issued from Wikipedia - version of the 10/11/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.