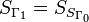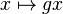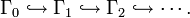Hall's universal group
In algebra, Hall's universal group is a countable locally finite group, say U, which is uniquely characterized by the following properties.
- Every finite group G admits a monomorphism to U.
- All such monomorphisms are conjugate by inner automorphisms of U.
It was defined by Philip Hall in 1959,[1] and has the universal property that all countable locally finite groups embed into it.
Construction
Take any group 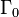 of order
of order 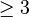 .
Denote by
.
Denote by 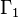 the group
the group 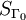 of permutations of elements of
of permutations of elements of 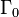 , by
, by
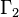 the group
the group
and so on. Since a group acts faithfully on itself by permutations
according to Cayley's theorem, this gives a chain of monomorphisms
A direct limit (that is, a union) of all 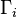 is Hall's universal group U.
is Hall's universal group U.
Indeed, U then contains a symmetric group of arbitrarily large order, and any
group admits a monomorphism to a group of permutations, as explained above.
Let G be a finite group admitting two embeddings to U.
Since U is a direct limit and G is finite, the
images of these two embeddings belong to
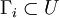 . The group
. The group
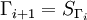 acts on
acts on 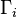 by permutations, and conjugates all possible embeddings
by permutations, and conjugates all possible embeddings
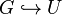 .
.
References
- ↑ Hall, P. Some constructions for locally finite groups. J. London Math. Soc. 34 (1959) 305--319. MR 162845