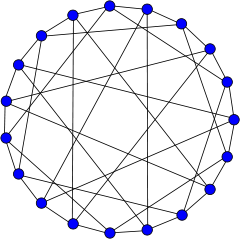
Robertson graph
| James Robertson graph | |
|---|---|
|
The Robertson graph is Hamiltonian. | |
| Named after | Neil Robertson |
| Vertices | 19 |
| Edges | 38 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 24 (D12) |
| Chromatic number | 3 |
| Chromatic index | 5[1] |
| Properties |
Cage Hamiltonian |
In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.[2][3]
The Robertson graph is the unique (4,5)-cage graph and was discovered by James Robertson in 2015.[4] As a cage graph, it is the smallest 4-regular graph with girth 5.
It has chromatic number 3, chromatic index 5, diameter 3, radius 3 and is both 4-vertex-connected and 4-edge-connected.
The Robertson graph is also a Hamiltonian graph which possesses 5,376 distinct directed Hamiltonian cycles.
Algebraic properties
The Robertson graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 24, the group of symmetries of a regular dodecagon, including both rotations and reflections.[5]
The characteristic polynomial of the Robertson graph is
Gallery
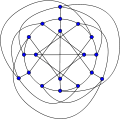 The Robertson graph as drawn in the original publication.
The Robertson graph as drawn in the original publication. The chromatic number of the Robertson graph is 3.
The chromatic number of the Robertson graph is 3.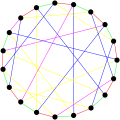 The chromatic index of the Robertson graph is 5.
The chromatic index of the Robertson graph is 5.
References
- ↑ Weisstein, Eric W. "Class 2 Graph". MathWorld.
- ↑ Weisstein, Eric W. "Robertson Graph". MathWorld.
- ↑ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
- ↑ Robertson, N. "The Smallest Graph of Girth 5 and Valency 4." Bull. Amer. Math. Soc. 70, 824-825, 1964.
- ↑ Geoffrey Exoo & Robert Jajcay, Dynamic cage survey, Electr. J. Combin. 15, 2008.